a C# learning space

Buy me a cup of coffee?

•   Home  
•   C# Basics  
•   Creating an Interface  
•   Painting the Form  
•   Creating Grid & Cell Objects
•   Let's Get Coding
•   Sudoku Terminology  
•   Sudoku Strategies  

Strategies

To solve a Sudoku puzzle, you need the process of elimination. By eliminating all possible outcomes except one, you are able to solve the puzzle one cell at a time. If you've played Sudoku, you probably used some of these strategies without even realizing it.
Below are basic strategies for solving Sudoku. They are listed in order of difficulty. It starts with the easiest methods for solving and work towards the harder methods. If you need to use methods that are harder in order to solve a puzzle, the difficulty level of the puzzle increases.

• Naked Single

  • A Naked Single is an unsolved cell that only has one possible candidate. That candidate is the solution to that cell. Below is an example of Naked Singles. There are two Naked Singles within the 8th column and 9th box. By solving these two cells, it also eleminates the 1 and the 9 in their respective peers.
    
    

• Hidden Single

  • A Hidden Single is a lone candidate with a row, column, or box. Meaning that there is only one cell within the row, column, or box with the lone candidate. Below is an example of a Hiddle Single. In this case the lone candidate is a 5. There are no other cells within it's peer row, column, and box. Although only one of these need to exist for the 5 to be considered a Hidden Single. It is said to be hidden, because there is another candidate within the same cell.
    
    

• Naked Pair

  • Naked Pairs are two cells within a peer row, column, or box that have the same pair of candidates. Below is an example of a Naked Pair.
    
    

• Locked Candidate Pointing

  • When considering whether a Locked Candidate exists, you will want to focus on the boxes. The first type of Locked Candidate has a single row or column within a box where a candidate is only valid within that row or column. When a candidate exists in this situation the rest of the peer row or column cannot have that candidate since it can only be valid within the box. So, the candidate is said to be pointing to invalid candidates. In the example below the 1s in box 3 that are highlighted are the only 1s as candidates within that box. So, the column in which they "point" show that the other 1s in that column can be disqualified as valid solutions.
    
    

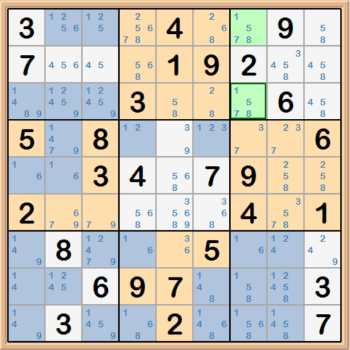
• Locked Candidate Claiming

  • Locked Candidate Claiming is similar to the Locked Candidate Pointing, but you look at the a row or column and if a candidate only exists with a box within that row or column, then the rest of the candidates within the peer box cannot exist as a valid solution. In the example below, take a look at column 8 and box 6. The 2s in the column only exist in box 8. So, one of those two cells have to be a 2 and the other cells that have 2 as a candidate can have the 2 eliminated as a possible solution.
    
    

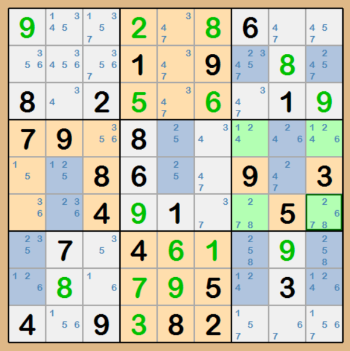
• Naked Triple

  • Naked Triples are pretty much the same thing as Naked Pairs, except they involve three cells and three candidates. Not all cells have to contain three candidates, but the combination of the cells can only contain three candidates. In the example below, there are three cells highlighted that contain Naked Triples (4, 5, & 6). But two of the cells only contain pairs.
    
    

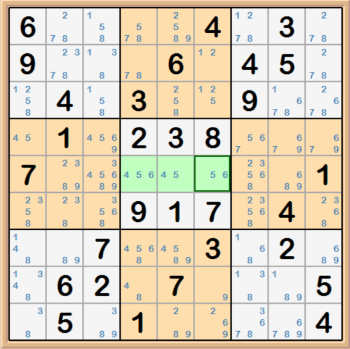
• Hidden Pair

  • Hidden Pairs are two cells within a peer row, column, or box where neither of the candidates of that pair are contained in any other cell within that peer row, column, or box. But they do contain other candidates. The other candidates "hide" that fact that the pair are the only possible solutions to that cell. In the example below the second row contains two cells that are highlighted that contain a 2 and a 3, where the rest of the row has no 2 or 3 in any of the other cells. So, all of the candidates other than the 2 & 3 within the highlighted cells can be disqualified as valid solutions.
    
    

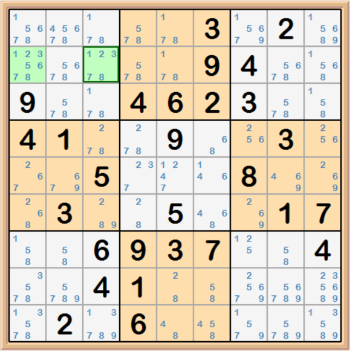
• Hidden Triple

  • Hidden Triples are very much the same as Hidden Pairs, but with three cells and three candidates rather than two. In the example below the 7, 8, and 9 in the three highlighted cells form a hidden triple in box 8. Probably not the best example since there are easier to see solutions in that same box. But it illustrates the idea. Once a hidden triple is found, you can disqualify the other candidates within the three highlighted cells since none of them would provide a valid solution to the puzzle.
    
    

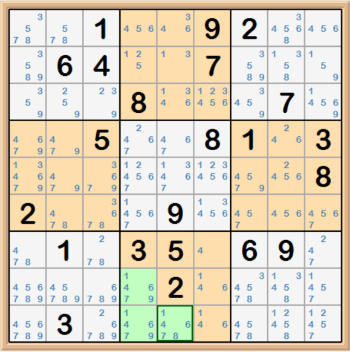
• X-Wing

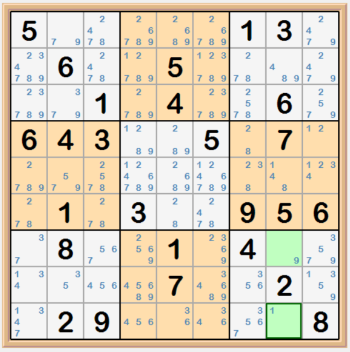
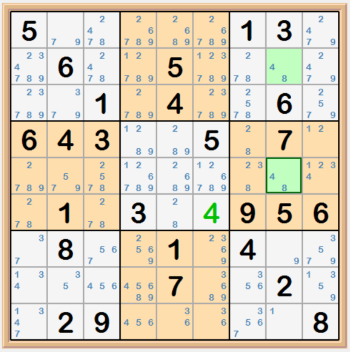
  • An X-Wing consists of four cells that form a rectangle where the corners of the rectangle are the cells. In the example below, the green highligted cells focus on the 1s candidates and have two cells in row 6 that are the only cells to contain 1s and two cells in row 8 that are the only cells in that row to contain 1s. These cells have peers in columns 3 and 4. Because the 1s can only be in green highlighted cells, the two cells highlighted in red, cannot have 1s as a candidate within columns 3 and 4. The second image shows how we get the X in the X-Wing.
    
    

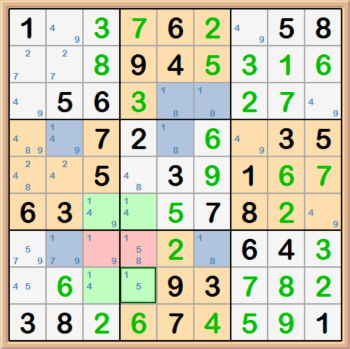
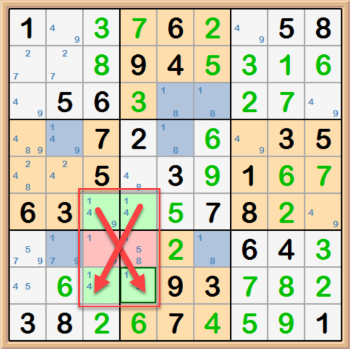
• Swordfish

  • Pairs work with two candidates and Triplets work with three candidates. X-Wing works with pairs of cells and Swordfish just expands on that with three sets of cells. The cells of each row, need to also share columns in both X-Wing and Swordfish (and Jellyfish (4 cells) and Squirmbag (5 cells)).
    
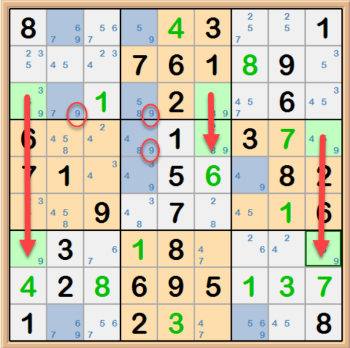
    A Swordfish consists of three rows or three columns with either two or three cells containing a particular candidate. Below I am looking at the 9s. The three rows or columns must have the same corrisponding column or row peers. It kind of forms a three by three rectangle on the grid. Because the grouping of candidates in the rows, any cells containing that candidate within the peer columns can be disqualified as valid candidates. The same idea applies to the column relationship and other peer rows containing the candidate.
    
    Below are three images of the same puzzle. The first image is highlighting the possible 9s after solving some of the puzzle. The second image shows a Swordfish example in rows. And the thrid image shows a Swordfish example in columns. I've flagged the 9s that can be deleted and by circling them. As you can see, it doesn't matter which of the two Swordfish techniques you use, it disqualifies the same 9s.
    
    

• XY-Wing

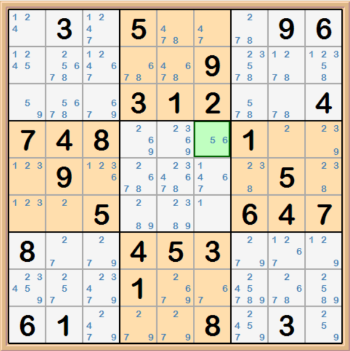
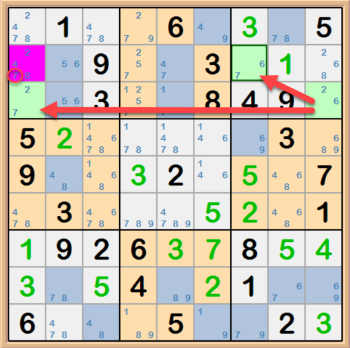
  • XY-Wings are a way to look at associated pairs of candidates in three cells, one of which is a peer to the other two, but the other two are not peers to each other. The pivoting cell (peer to the other two) would have candidates XY and the other two cells would have candidates XZ and YZ. Then you can disqualify the Z candidate from the cell where XZ and YZ intersect (not the pivoting cell though). Let's take a look at an example.
    
    Below the three cells that make up the XY-Wing are highlighted in green. When you think about what combinations can make a valid solution to these three cells, it makes sense that you can disqalify the 7 in the purple cell. In row 3 and column 9 the cell can only contain a 2 or a 6. If it is a 2, then the cell in row 3 and column 1 would have to be a 7, which would disqalify the 7 in the purple cell. And if the value in row 3 and column 9 were the 6, then the value in the cell at row 2 and column 7 would have to be a 7. Either way the 7 in the purple cell is disqualified.
    
    A easy way to find XY-Wing pairs is to highlight all of the cells that have pairs and just keep looking for the right combination. When you find and solve an XY-Wing, there is a very good chance the rest of the puzzle comes pretty easy. That being said, there is one more XY-Wing in the example below. If you can find it, the rest of the puzzle is pretty easy.
    
    

• Chaining

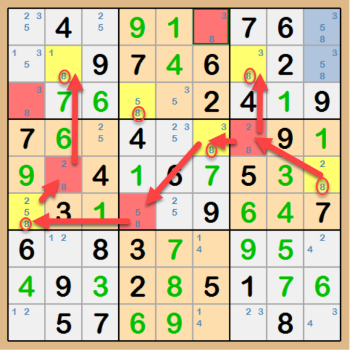
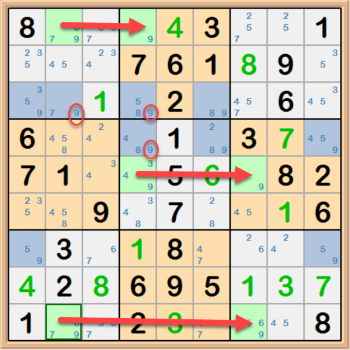
  • Tracking the possible chaining of a single candidate can sometimes help to disqualifying candidates within cells. Take a look at the example below. Highlighting pairs of cells with alternating colors will identify chains of that candidate. If one cell contains that candidate, the only other peer cell cannot contain that candidate and vise versa. Following the chain until it comes back on itself and you have two cells that have the same candidate tells you that the candidate can be eliminated where the conflict occurs. In this case the yellow cells containing 8s can all have the 8 disqualified because the chain has a conflict in the second row. Both cells cannot be 8. This also means that the 8 has to exist in the 9th cell in the 2nd row.